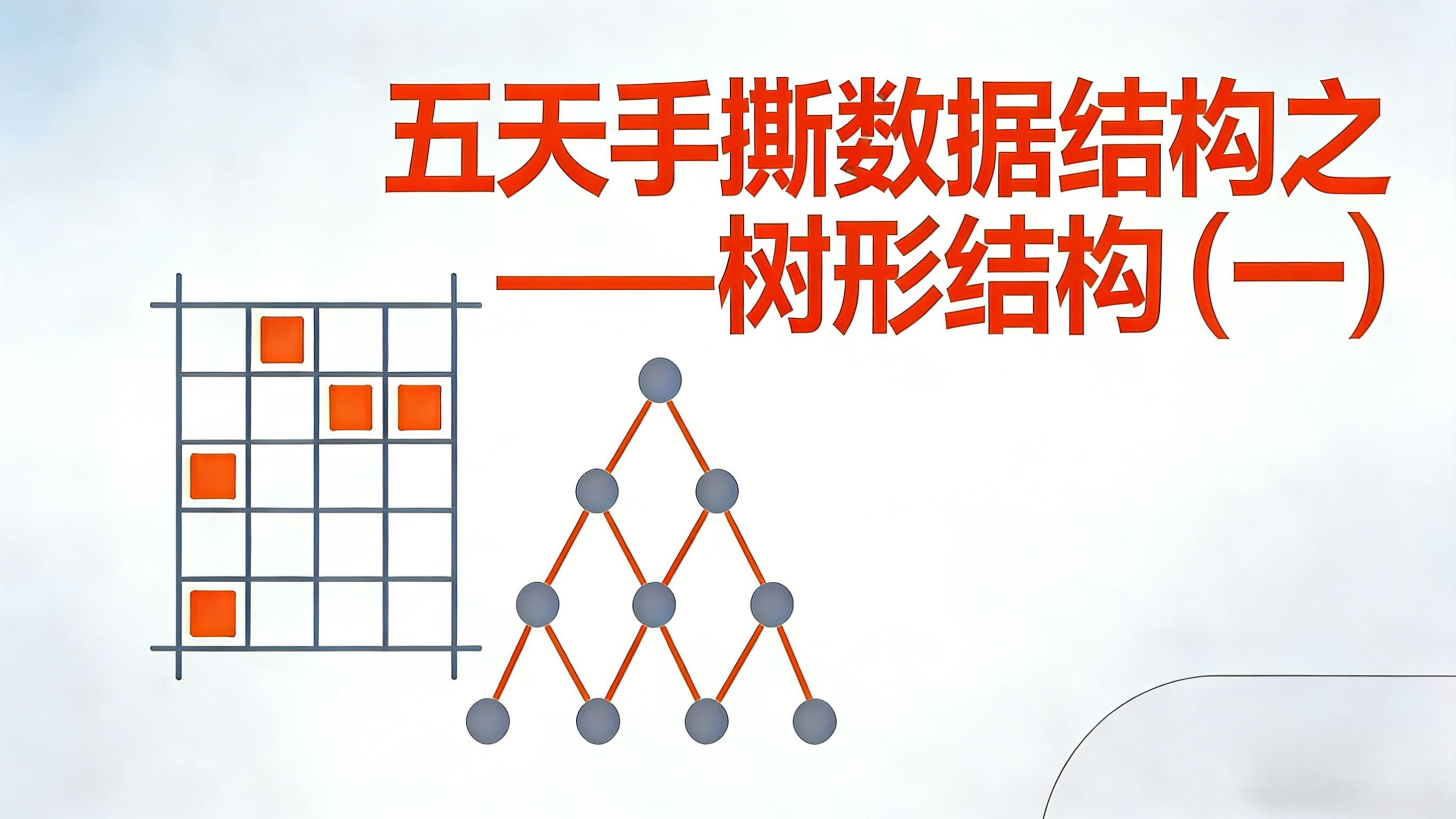
五天手撕数据结构之——线性结构

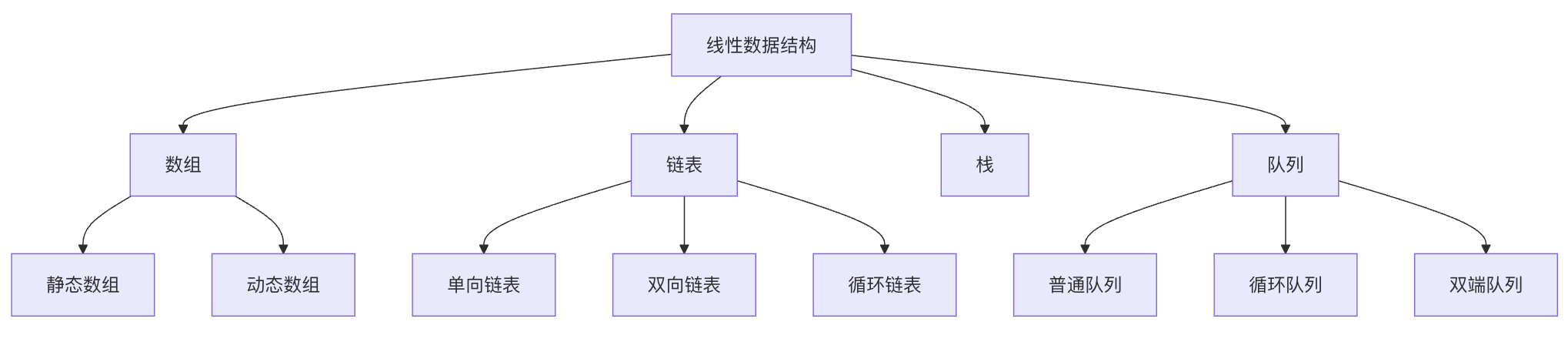
线性结构概论

线性的数据结构元素之间是一对一的关系。

除了第一个元素，所有的元素都只有唯一前驱；

除了最后一个元素所有的元素都有唯一的后继。

常见的数据结构：

• 数组：像一排带有编号的储物柜，每个柜子都有自己的位置和相应的编号
• 链表：像一列拥堵的车流，每辆车只能知道前后的车辆编号
• 栈：像一叠盘子，只能从顶部取和放
• 队列：像是排队买票，最前面的最先消费

数组：数据的固定存放柜

数组是最简单最直接的线性数据结构

我们可以把他想象成一排储物柜

基本概念和特点：

• 连续存储：数组在内存中占据一块连续的空间，就像每个储物柜都是紧挨着的
• 固定大小：数组在创建时就已经确定了其容量（长度），之后通常不能改变，就像打好的柜子不能再改变大小
• 索引访问：每个元素都有自己的唯一编号，称为索引。在大多数编程语言中，索引从0开始，在查找数据是可以通过索引号快速访问任何一个元素，时间复杂度为O(1)

下面使用java语言的ArrayList（动态数组）演示数组的增删改查

public static void main(String[] args) {
    // 1.创建数组
    List<String> cabinet = new ArrayList<String>() {{
        add("101-肥皂");
        add("102-衣服");
        add("103-饭盒");
        add("104-空");
        add("105-空");
    }};
    System.out.println("柜子存放情况："+cabinet);

    // 2.访问102
    // 查看102存放的东西
    String string = cabinet.get(1);
    System.out.println("102柜子中存放的是："+string);

    // 3.更新元素
    // 向104中放置东西
    cabinet.set(3,"104-酱油");
    System.out.println("104放入东西后："+cabinet);

    // 4.新增元素
    // 焊接一个格
    cabinet.add("106-空");
    System.out.println("新柜子："+cabinet);

    // 5.删除一个元素
    // 砍掉一个格
    cabinet.remove(3);
    System.out.println("砍掉一个格之后："+cabinet);
}

//柜子存放情况：[101-肥皂, 102-衣服, 103-饭盒, 104-空, 105-空]
//102柜子中存放的是：102-衣服
//104放入东西后：[101-肥皂, 102-衣服, 103-饭盒, 104-酱油, 105-空]
//新柜子：[101-肥皂, 102-衣服, 103-饭盒, 104-酱油, 105-空, 106-空]
//砍掉一个格之后：[101-肥皂, 102-衣服, 103-饭盒, 105-空, 106-空]

优点和缺点：

优点

• 高速随机访问：通过索引可直接访问任何元素
• 内存效率高：连续存储，无需额外存储元素关联关系

缺点

• 大小固定：静态数组一旦创建，容量难以改变
• 插入删除成本高：在中间插入或删除元素需要移动大量后续元素以保持连续性

链表：数据的火车车厢

当数组的固定大小和插入删除的低效成为问题时，链表就登场了。链表像一列火车，每节车厢（节点）都装载着货物（数据），并通过挂钩（指针）连接下一节车厢。

如图所示头指针指向节点A每个节点的Next指针指向下一个节点，最后一个节点的Next指向Null表示结束

链表主要类型：

• 单向链表：节点只指向下一个节点
• 双向链表：节点同时指向前一个和后一个节点，可以双向遍历
• 循环链表：尾节点执行头节点，形成一个环

java实现单向链表

package com.springdemo.demo;

/**
 * 单向链表节点类
 * 泛型设计，支持存储任意类型数据
 */
class Node<T> {
    // 数据域：存储节点值
    T data;
    // 指针域：指向下一个节点
    Node<T> next;

    // 构造方法：初始化节点数据
    public Node(T data) {
        this.data = data;
        this.next = null; // 初始时下一个节点为null
    }
}

/**
 * 单向链表实现类
 */
public class SinglyLinkedList<T> {
    // 头节点（链表的入口，初始为null）
    private Node<T> head;
    // 链表长度（记录节点数量，避免每次遍历统计）
    private int size;

    // 构造方法：初始化空链表
    public SinglyLinkedList() {
        this.head = null;
        this.size = 0;
    }

    /**
     * 1. 判断链表是否为空
     * @return 空返回true，否则返回false
     */
    public boolean isEmpty() {
        return size == 0;
    }

    /**
     * 2. 获取链表长度
     * @return 节点数量
     */
    public int size() {
        return size;
    }

    /**
     * 3. 向链表尾部添加节点
     * @param data 要添加的节点数据
     */
    public void add(T data) {
        // 创建新节点
        Node<T> newNode = new Node<>(data);
        // 链表为空时，新节点作为头节点
        if (head == null) {
            head = newNode;
        } else {
            // 链表非空时，遍历到尾部节点
            Node<T> current = head;
            while (current.next != null) {
                current = current.next;
            }
            // 尾部节点指向新节点
            current.next = newNode;
        }
        size++; // 长度+1
    }

    /**
     * 4. 在指定索引位置插入节点（索引从0开始）
     * @param index 插入位置
     * @param data  插入数据
     * @throws IndexOutOfBoundsException 索引越界时抛出异常
     */
    public void add(int index, T data) {
        // 校验索引合法性
        if (index < 0 || index > size) {
            throw new IndexOutOfBoundsException("索引越界：" + index + "，链表长度：" + size);
        }
        // 创建新节点
        Node<T> newNode = new Node<>(data);
        // 插入到头部（索引0）
        if (index == 0) {
            newNode.next = head; // 新节点指向原头节点
            head = newNode;      // 头节点更新为新节点
        } else {
            // 找到插入位置的前一个节点
            Node<T> prev = head;
            for (int i = 0; i < index - 1; i++) {
                prev = prev.next;
            }
            // 新节点指向前一个节点的下一个节点
            newNode.next = prev.next;
            // 前一个节点指向新节点
            prev.next = newNode;
        }
        size++; // 长度+1
    }

    /**
     * 5. 删除指定索引位置的节点
     * @param index 要删除的索引
     * @return 被删除节点的数据
     * @throws IndexOutOfBoundsException 索引越界时抛出异常
     */
    public T remove(int index) {
        // 校验索引合法性
        if (index < 0 || index >= size) {
            throw new IndexOutOfBoundsException("索引越界：" + index + "，链表长度：" + size);
        }
        Node<T> removeNode;
        // 删除头节点（索引0）
        if (index == 0) {
            removeNode = head;
            head = head.next; // 头节点指向原第二个节点
        } else {
            // 找到删除位置的前一个节点
            Node<T> prev = head;
            for (int i = 0; i < index - 1; i++) {
                prev = prev.next;
            }
            removeNode = prev.next;
            // 前一个节点跳过被删除节点，指向其后继节点
            prev.next = removeNode.next;
        }
        size--; // 长度-1
        return removeNode.data; // 返回被删除的数据
    }

    /**
     * 6. 查找指定索引位置的节点数据
     * @param index 查找索引
     * @return 对应位置的数据
     * @throws IndexOutOfBoundsException 索引越界时抛出异常
     */
    public T get(int index) {
        // 校验索引合法性
        if (index < 0 || index >= size) {
            throw new IndexOutOfBoundsException("索引越界：" + index + "，链表长度：" + size);
        }
        // 遍历到指定索引节点
        Node<T> current = head;
        for (int i = 0; i < index; i++) {
            current = current.next;
        }
        return current.data;
    }

    /**
     * 7. 遍历链表，输出所有节点数据
     */
    public void traverse() {
        if (isEmpty()) {
            System.out.println("链表为空");
            return;
        }
        Node<T> current = head;
        StringBuilder sb = new StringBuilder();
        sb.append("链表内容：");
        while (current != null) {
            sb.append(current.data).append(" -> ");
            current = current.next;
        }
        // 移除最后一个" -> "
        sb.delete(sb.length() - 4, sb.length());
        System.out.println(sb);
    }

    // 测试方法
    public static void main(String[] args) {
        // 创建String类型的单向链表
        SinglyLinkedList<String> list = new SinglyLinkedList<>();

        // 测试添加节点
        list.add("101");
        list.add("102");
        list.add("103");
        list.traverse(); // 输出：链表内容：101 -> 102 -> 103

        // 测试指定索引插入
        list.add(1, "104");
        list.traverse(); // 输出：链表内容：101 -> 104 -> 102 -> 103

        // 测试获取节点
        System.out.println("索引2的节点数据：" + list.get(2)); // 输出：102

        // 测试删除节点
        list.remove(1);
        list.traverse(); // 输出：链表内容：101 -> 102 -> 103

        // 测试长度和判空
        System.out.println("链表长度：" + list.size()); // 输出：3
        System.out.println("链表是否为空：" + list.isEmpty()); // 输出：false
    }
}

优点和缺点

优点：

• 动态大小：无需预先分配固定空间，可以灵活的增长和缩小
• 高效的插入/删除：在已知节点位置只需要球盖指针指向，无需移动大量元素

缺点：

• 内存开销大：每个节点需要额外空间存储指针
• 顺序访问：无法像数组一样直接通过索引访问，必须从头开始检索

栈：数据的叠盘子

栈是一种 后进先出 的数据结构，就像餐厅里叠放的盘子，你总是取走最后放上去的

栈只允许在一端（称为 栈顶）进行插入（入栈）和删除（出栈）操作。另一端称为 栈底。

核心操作：

• **push(data)**：将数据压入栈顶。
• **pop()**：弹出并返回栈顶元素。
• **peek() / top()**：查看栈顶元素但不弹出。
• **is_empty()**：检查栈是否为空。

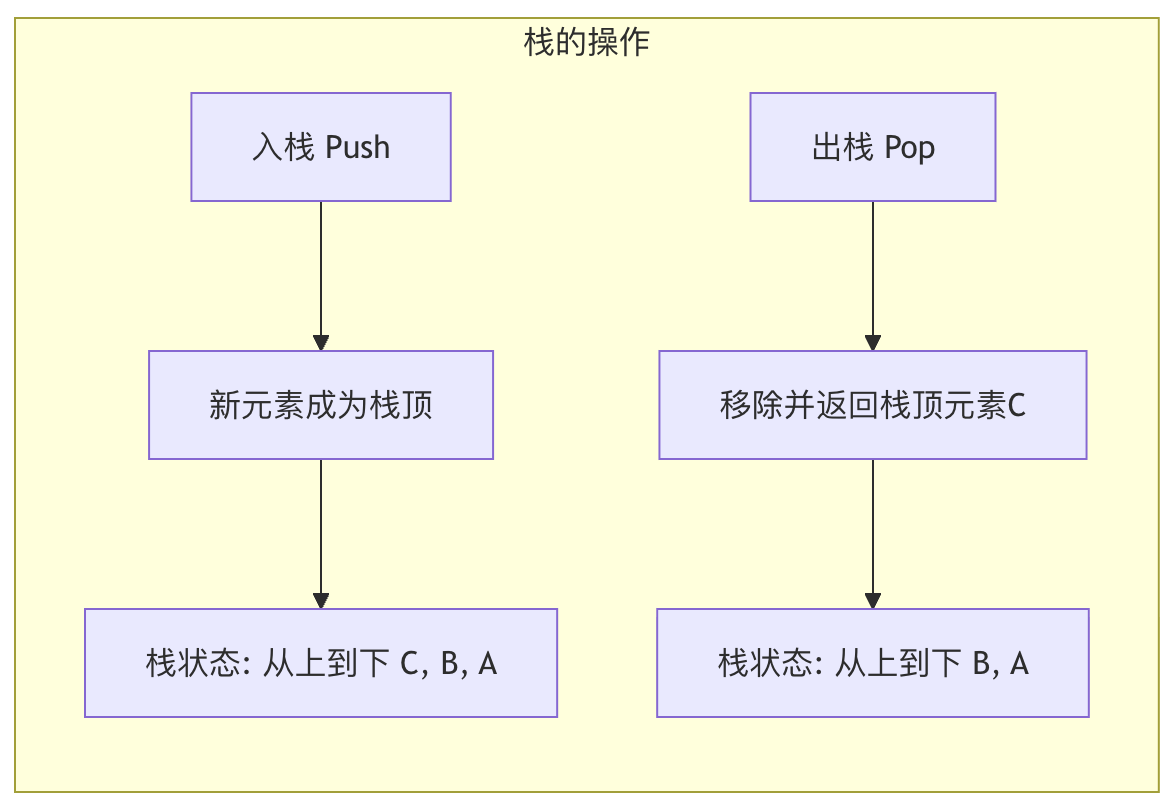
栈常被用于释放内存，撤销更改，浏览器前进后退，括号匹配等

java实现数组版本栈

/**
 * 基于数组实现的栈（泛型设计，支持任意数据类型）
 */
public class ArrayStack<T> {
    // 底层存储元素的数组
    private Object[] stack;
    // 栈顶指针（初始为-1，表示空栈）
    private int top;
    // 栈的初始容量
    private static final int DEFAULT_CAPACITY = 10;

    // 构造方法：初始化默认容量的栈
    public ArrayStack() {
        stack = new Object[DEFAULT_CAPACITY];
        top = -1;
    }

    // 构造方法：自定义初始容量
    public ArrayStack(int initialCapacity) {
        if (initialCapacity <= 0) {
            throw new IllegalArgumentException("初始容量必须大于0");
        }
        stack = new Object[initialCapacity];
        top = -1;
    }

    /**
     * 入栈：添加元素到栈顶
     * @param element 要入栈的元素
     */
    public void push(T element) {
        // 检查是否需要扩容（栈满时扩容为原容量的2倍）
        if (top == stack.length - 1) {
            resize(stack.length * 2);
        }
        // 栈顶指针上移，添加元素
        stack[++top] = element;
    }

    /**
     * 出栈：移除并返回栈顶元素
     * @return 栈顶元素
     * @throws RuntimeException 栈空时抛出异常
     */
    @SuppressWarnings("unchecked")
    public T pop() {
        if (isEmpty()) {
            throw new RuntimeException("栈为空，无法执行出栈操作");
        }
        // 获取栈顶元素，栈顶指针下移
        T element = (T) stack[top];
        stack[top--] = null; // 释放引用，帮助GC
        return element;
    }

    /**
     * 查看栈顶元素（不移除）
     * @return 栈顶元素
     * @throws RuntimeException 栈空时抛出异常
     */
    @SuppressWarnings("unchecked")
    public T peek() {
        if (isEmpty()) {
            throw new RuntimeException("栈为空，无栈顶元素");
        }
        return (T) stack[top];
    }

    /**
     * 判断栈是否为空
     * @return 空返回true，否则返回false
     */
    public boolean isEmpty() {
        return top == -1;
    }

    /**
     * 获取栈的大小
     * @return 元素数量
     */
    public int size() {
        return top + 1;
    }

    /**
     * 数组扩容/缩容（私有方法，内部调用）
     * @param newCapacity 新容量
     */
    private void resize(int newCapacity) {
        Object[] newStack = new Object[newCapacity];
        // 复制原数组元素到新数组
        System.arraycopy(stack, 0, newStack, 0, top + 1);
        stack = newStack;
    }

    // 测试方法
    public static void main(String[] args) {
        ArrayStack<String> stack = new ArrayStack<>();

        // 入栈
        stack.push("101");
        stack.push("102");
        stack.push("103");
        System.out.println("栈大小：" + stack.size()); // 输出：3
        System.out.println("栈顶元素：" + stack.peek()); // 输出：103

        // 出栈
        String popElement = stack.pop();
        System.out.println("出栈元素：" + popElement); // 输出：103
        System.out.println("出栈后栈大小：" + stack.size()); // 输出：2

        // 判空
        System.out.println("栈是否为空：" + stack.isEmpty()); // 输出：false

        // 清空栈
        stack.pop();
        stack.pop();
        System.out.println("清空后栈是否为空：" + stack.isEmpty()); // 输出：true
    }
}

栈的核心优势：O (1) 的操作效率 + 天然贴合 “后进先出” 场景 + 安全可控的封装性

队列：数据的排队通道

队列是一种 先进先出 的数据结构，就像生活中任何需要排队的地方（如超市收银台），先来的人先接受服务。

队列允许在一端（称为 队尾）进行插入（入队）操作，在另一端（称为 队头）进行删除（出队）操作。

核心操作：

• **enqueue(data)**：将数据加入队尾。
• **dequeue()**：从队头移除并返回数据。
• **front() / peek()**：查看队头数据但不移除。
• **is_empty()**：检查队列是否为空。

队列常用于需要按顺序处理任务的场景，如：打印任务队列、消息队列、广度优先搜索等。

java循环数组实现队列

/**
 * 基于循环数组实现的队列（泛型设计）
 */
public class ArrayQueue<T> {
    // 底层存储元素的数组
    private Object[] queue;
    // 队首指针（指向队首元素的下标）
    private int front;
    // 队尾指针（指向队尾下一个可插入的下标）
    private int rear;
    // 队列元素数量
    private int size;
    // 默认初始容量
    private static final int DEFAULT_CAPACITY = 10;

    // 构造方法：初始化默认容量队列
    public ArrayQueue() {
        queue = new Object[DEFAULT_CAPACITY];
        front = 0;
        rear = 0;
        size = 0;
    }

    // 构造方法：自定义初始容量
    public ArrayQueue(int initialCapacity) {
        if (initialCapacity <= 0) {
            throw new IllegalArgumentException("初始容量必须大于0");
        }
        queue = new Object[initialCapacity];
        front = 0;
        rear = 0;
        size = 0;
    }

    /**
     * 入队：向队尾添加元素
     * @param element 要入队的元素
     */
    public void enqueue(T element) {
        // 队列满时扩容（扩容为原容量的2倍）
        if (size == queue.length) {
            resize(queue.length * 2);
        }
        // 元素放入队尾指针位置
        queue[rear] = element;
        // 队尾指针循环后移（取模避免越界）
        rear = (rear + 1) % queue.length;
        size++;
    }

    /**
     * 出队：移除并返回队首元素
     * @return 队首元素
     * @throws RuntimeException 队列为空时抛出异常
     */
    @SuppressWarnings("unchecked")
    public T dequeue() {
        if (isEmpty()) {
            throw new RuntimeException("队列为空，无法执行出队操作");
        }
        // 获取队首元素
        T element = (T) queue[front];
        // 释放队首位置引用，帮助GC
        queue[front] = null;
        // 队首指针循环后移
        front = (front + 1) % queue.length;
        size--;
        return element;
    }

    /**
     * 查看队首元素（不移除）
     * @return 队首元素
     * @throws RuntimeException 队列为空时抛出异常
     */
    @SuppressWarnings("unchecked")
    public T peek() {
        if (isEmpty()) {
            throw new RuntimeException("队列为空，无队首元素");
        }
        return (T) queue[front];
    }

    /**
     * 判断队列是否为空
     */
    public boolean isEmpty() {
        return size == 0;
    }

    /**
     * 获取队列大小
     */
    public int size() {
        return size;
    }

    /**
     * 数组扩容（私有方法）
     * @param newCapacity 新容量
     */
    private void resize(int newCapacity) {
        Object[] newQueue = new Object[newCapacity];
        // 复制原队列元素到新数组（按顺序从front开始复制）
        for (int i = 0; i < size; i++) {
            newQueue[i] = queue[(front + i) % queue.length];
        }
        // 重置指针和数组
        queue = newQueue;
        front = 0;
        rear = size;
    }

    // 测试方法
    public static void main(String[] args) {
        ArrayQueue<String> queue = new ArrayQueue<>();

        // 入队
        queue.enqueue("101");
        queue.enqueue("102");
        queue.enqueue("103");
        System.out.println("队列大小：" + queue.size()); // 输出：3
        System.out.println("队首元素：" + queue.peek()); // 输出：101

        // 出队
        String deqElement = queue.dequeue();
        System.out.println("出队元素：" + deqElement); // 输出：101
        System.out.println("出队后队列大小：" + queue.size()); // 输出：2

        // 判空
        System.out.println("队列是否为空：" + queue.isEmpty()); // 输出：false

        // 清空队列
        queue.dequeue();
        queue.dequeue();
        System.out.println("清空后队列是否为空：" + queue.isEmpty()); // 输出：true
    }
}

如何选择？

• 需要 快速随机访问 和已知数据量时，选择 数组。
• 需要 频繁在任意位置插入或删除 元素，且数据量变化大时，选择 链表。
• 需要实现 “撤销” 功能或 反向处理 顺序时，考虑 栈。
• 需要按 “先来后到” 的顺序处理任务时，使用 队列。