五天手撕数据结构之——树形结构（一）

树形结构概论

树（Tree）是一种非线性的数据结构，它模拟了自然界中树的分支层次，与数组、链表这种一个接一个的线性结构不同，树中的数据元素（称为节点）之间存在明确的一对多的层次关系

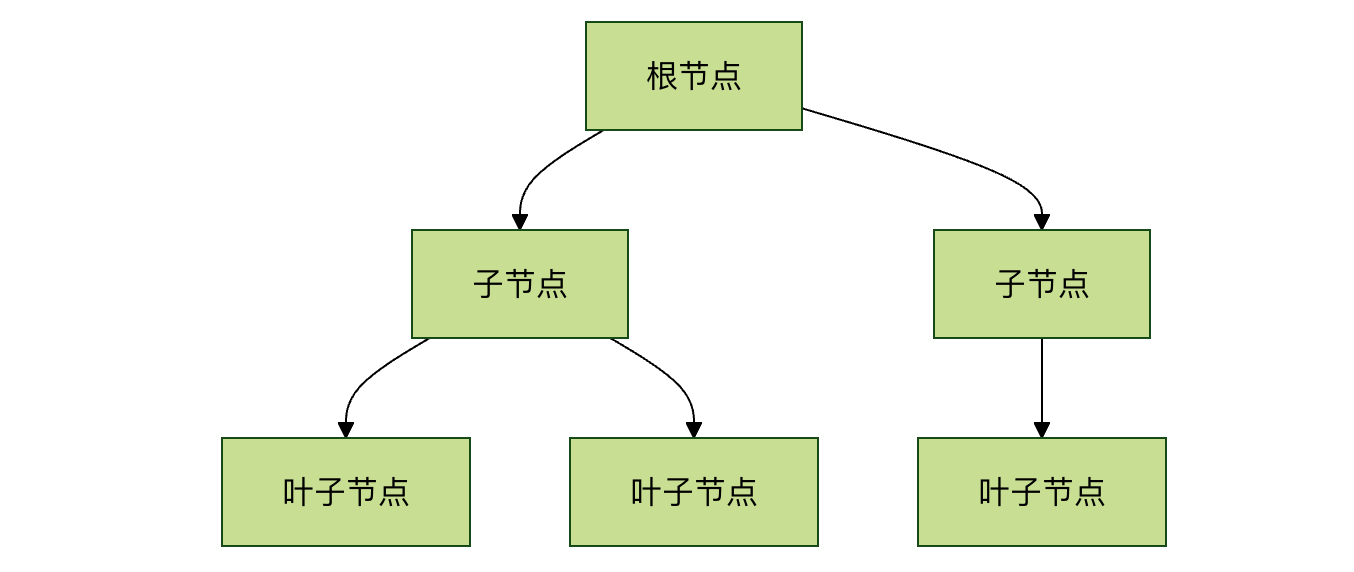
树形结构就像一棵树：

  • 根节点：树的根部，唯一没有父节点的节点
  • 子节点：从某个节点分支出去的节点
  • 叶节点：没有子节点的节点，像树叶
  • 路径：从一个节点到另一个节点的路线
  • 深度：从根节点到该节点的路径长度
  • 高度：从该节点到最远叶节点的路径长度

生活比喻：

  • 家族树：祖父母→父母→子女→孙子女
  • 组织架构：CEO→总监→经理→员工
  • 文件系统：根目录→子目录→文件
结构类型 查找效率 插入效率 删除效率 有序性
数组 O(n) O(n) O(n) 无
链表 O(n) O(1) O(1) 无
哈希表 O(1) O(1) O(1) 无
二叉搜索树 O(log n) O(log n) O(log n) 有

树的基本模型：

树的基本结构

树的基本性质

  1. 唯一路径：树中任意两个节点之间有且仅有一条路径。
  2. N 个节点，N-1 条边：一棵具有 N 个节点的树，总共有 N-1 条边。
  3. 无环：树中不存在环（即从某个节点出发，沿着边最终又能回到该节点）。

为什么需要树？

你可能会问，有了数组和链表，为什么还需要树？答案在于效率。

  • 数组：查找快（通过索引），但插入和删除慢（需要移动大量元素）。

  • 链表：插入和删除快，但查找慢（需要从头遍历）。

  • 树（特别是二叉搜索树）：在保持数据有序的同时，能提供比链表快得多的搜索速度，以及比数组更高效的插入/删除操作。

二叉树：树家族中最重要的一员

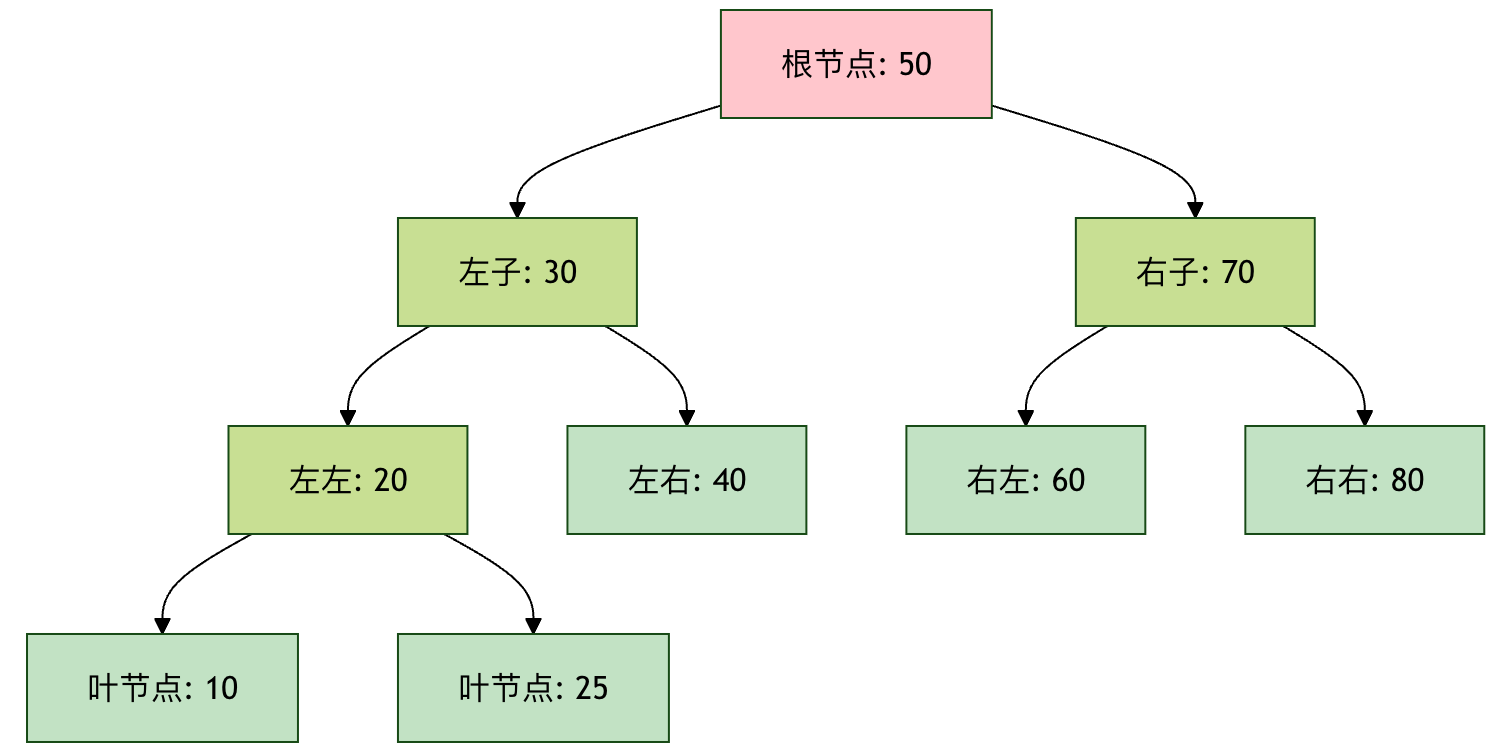
二叉树（Binary Tree）是每个节点最多有两个子节点的树，这两个子节点通常被称为左子节点和右子节点，它是许多强大树结构（如二叉搜索树、堆、AVL 树）的基础。

基本结构如下：

二叉树示意图

java实现中序二叉树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
package com.springdemo.demo.binarytree;

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    public TreeNode(int val) {
        this.val = val;
        this.left = null;
        this.right = null;
    }
}

public class BinaryTreeDemo {
    public static void main(String[] args) {
        // 手动构建如下树：
        //       1
        //      / \
        //     2   3
        //    / \
        //   4   5

        TreeNode root = new TreeNode(1);
        root.left = new TreeNode(2);
        root.right = new TreeNode(3);
        root.left.left = new TreeNode(4);
        root.left.right = new TreeNode(5);

        // 遍历验证
        inorder(root); // 输出: 4 2 5 1 3
    }

    // 中序遍历（递归）
    public static void inorder(TreeNode node) {
        if (node != null) {
            inorder(node.left);
            System.out.print(node.val + " ");
            inorder(node.right);
        }
    }
}

二叉搜索树：有秩序的二叉树

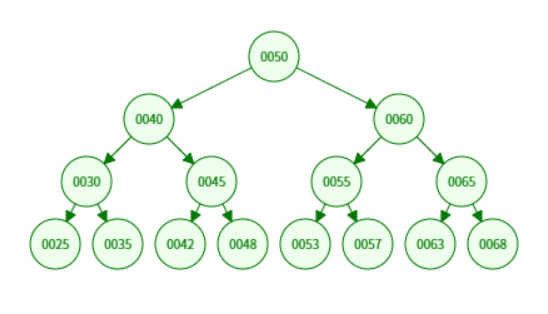
二叉搜索树（Binary Search Tree，简称 BST）是一种特殊的二叉树，它在普通二叉树的基础上增加了有序性约束，使得查找、插入、删除等操作可以高效进行。

基本概念和特点：

对于任意节点 node：

  • 若其左子树非空，则 左子树中所有节点的值 < node.val
  • 若其右子树非空，则 右子树中所有节点的值 > node.val
  • 左子树和右子树本身也必须是二叉搜索树
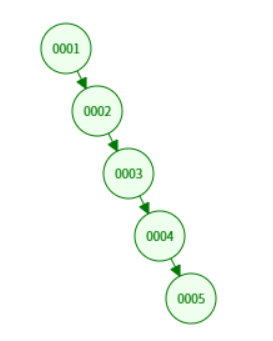
  • 若插入有序数据（如 1,2,3,4,5），BST 会退化为链表，h = n，性能降至 O(n)

二叉搜索树理想情况不理想情况退化成链表

java实现二叉搜索树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
package com.springdemo.demo.binarytree;

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode(int val) {
        this.val = val;
    }
}

public class BalancedBinaryTree{

    // 查找指定元素
    public boolean search(TreeNode root, int target) {
        if (root == null) return false;
        if (target == root.val) return true;
        if (target < root.val) {
            return search(root.left, target);
        } else {
            return search(root.right, target);
        }
    }

    // 插入元素
    public TreeNode insert(TreeNode root, int val) {
        if (root == null) {
            return new TreeNode(val); // 插入位置
        }
        if (val < root.val) {
            root.left = insert(root.left, val);
        } else if (val > root.val) {
            root.right = insert(root.right, val);
        }
        // val == root.val 时通常不插入（去重）
        return root;
    }

    // 删除元素分三种情况：
    // 叶子节点：直接删除
    // 只有一个子节点：用子节点替代
    // 有两个子节点：用中序前驱（左子树最大值）或中序后继（右子树最小值）替换，再删除那个前驱/后继
    public TreeNode delete(TreeNode root, int key) {
        if (root == null) return null;

        if (key < root.val) {
            root.left = delete(root.left, key);
        } else if (key > root.val) {
            root.right = delete(root.right, key);
        } else {
            // 找到要删除的节点
            if (root.left == null) return root.right;
            if (root.right == null) return root.left;

            // 有两个子节点：用右子树的最小值（中序后继）替代
            TreeNode successor = findMin(root.right);
            root.val = successor.val;
            root.right = delete(root.right, successor.val);
        }
        return root;
    }

    private TreeNode findMin(TreeNode node) {
        while (node.left != null) {
            node = node.left;
        }
        return node;
    }
}