五天手撕数据结构之——树形结构（二）

AVL 树：高度平衡的守护者

AVL 树是最早被发明的自平衡二叉搜索树，以其发明者 Adelson-Velsky 和 Landis 的名字命名。

AVL 树的核心思想非常简单：对于树中的任意一个节点，其左子树和右子树的高度差不能超过 1。

基本概念和特点：

  • 严格平衡：对于任意节点，其左子树与右子树的高度差（称为“平衡因子”）的绝对值 ≤ 1
  • **高度始终为 O(log n)**：由于严格平衡，AVL 树的高度最多约为 1.44 × log₂(n + 2) - 0.328
  • 每个节点需存储高度或平衡因子：为了快速判断是否失衡，通常在节点中额外存储：子树高度（height），或平衡因子（bf = left.height - right.height）

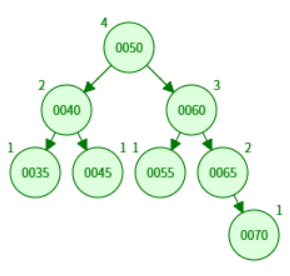
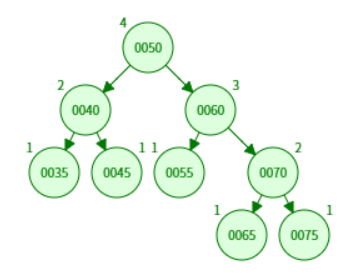
如图，插入75之后右侧右右失衡，执行左旋转

未插入75之前插入75之后

java版本实现AVL树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
package com.springdemo.demo.binarytree;

class AVLNode {
    int val;
    int height;          // 子树高度（叶子节点高度为 1）
    AVLNode left, right;

    public AVLNode(int val) {
        this.val = val;
        this.height = 1; // 新节点高度为 1
    }
}

public class AVLTree {
    private AVLNode root;

    // 获取节点高度（空节点返回 0）
    private int height(AVLNode node) {
        return node == null ? 0 : node.height;
    }

    // 更新节点高度
    private void updateHeight(AVLNode node) {
        if (node != null) {
            node.height = 1 + Math.max(height(node.left), height(node.right));
        }
    }

    // 获取平衡因子：左子树高度 - 右子树高度
    private int getBalance(AVLNode node) {
        return node == null ? 0 : height(node.left) - height(node.right);
    }

    // ====== 旋转操作 ======

    // 右旋（LL 型）
    private AVLNode rotateRight(AVLNode y) {
        AVLNode x = y.left;
        AVLNode T2 = x.right;

        // 执行旋转
        x.right = y;
        y.left = T2;

        // 更新高度（先更新子节点，再父节点）
        updateHeight(y);
        updateHeight(x);

        return x; // 新根
    }

    // 左旋（RR 型）
    private AVLNode rotateLeft(AVLNode x) {
        AVLNode y = x.right;
        AVLNode T2 = y.left;

        // 执行旋转
        y.left = x;
        x.right = T2;

        // 更新高度
        updateHeight(x);
        updateHeight(y);

        return y; // 新根
    }

    // ====== 插入操作 ======
    public void insert(int val) {
        root = insertRec(root, val);
    }

    private AVLNode insertRec(AVLNode node, int val) {
        // 1. 执行普通 BST 插入
        if (node == null) {
            return new AVLNode(val);
        }

        if (val < node.val) {
            node.left = insertRec(node.left, val);
        } else if (val > node.val) {
            node.right = insertRec(node.right, val);
        } else {
            // 不允许重复值
            return node;
        }

        // 2. 更新当前节点高度
        updateHeight(node);

        // 3. 获取平衡因子
        int balance = getBalance(node);

        // 4. 如果失衡，分四种情况处理

        // Left Left (LL)
        if (balance > 1 && val < node.left.val) {
            return rotateRight(node);
        }

        // Right Right (RR)
        if (balance < -1 && val > node.right.val) {
            return rotateLeft(node);
        }

        // Left Right (LR)
        if (balance > 1 && val > node.left.val) {
            node.left = rotateLeft(node.left);
            return rotateRight(node);
        }

        // Right Left (RL)
        if (balance < -1 && val < node.right.val) {
            node.right = rotateRight(node.right);
            return rotateLeft(node);
        }

        // 未失衡，直接返回
        return node;
    }

    // ====== 删除操作 ======
    public void delete(int val) {
        root = deleteRec(root, val);
    }

    private AVLNode deleteRec(AVLNode node, int val) {
        // 1. 执行普通 BST 删除
        if (node == null) return null;

        if (val < node.val) {
            node.left = deleteRec(node.left, val);
        } else if (val > node.val) {
            node.right = deleteRec(node.right, val);
        } else {
            // 找到要删除的节点
            if (node.left == null || node.right == null) {
                AVLNode temp = (node.left != null) ? node.left : node.right;
                if (temp == null) {
                    // 叶子节点
                    temp = node;
                    node = null;
                } else {
                    // 有一个子节点
                    node = temp;
                }
            } else {
                // 有两个子节点：用中序后继（右子树最小值）替代
                AVLNode temp = minValueNode(node.right);
                node.val = temp.val;
                node.right = deleteRec(node.right, temp.val);
            }
        }

        if (node == null) return null;

        // 2. 更新高度
        updateHeight(node);

        // 3. 获取平衡因子
        int balance = getBalance(node);

        // 4. 四种旋转修复

        // Left Left
        if (balance > 1 && getBalance(node.left) >= 0) {
            return rotateRight(node);
        }

        // Left Right
        if (balance > 1 && getBalance(node.left) < 0) {
            node.left = rotateLeft(node.left);
            return rotateRight(node);
        }

        // Right Right
        if (balance < -1 && getBalance(node.right) <= 0) {
            return rotateLeft(node);
        }

        // Right Left
        if (balance < -1 && getBalance(node.right) > 0) {
            node.right = rotateRight(node.right);
            return rotateLeft(node);
        }

        return node;
    }

    // 查找最小值节点（用于删除）
    private AVLNode minValueNode(AVLNode node) {
        AVLNode current = node;
        while (current.left != null) {
            current = current.left;
        }
        return current;
    }

    // ====== 遍历与工具方法 ======
    public void inorder() {
        System.out.print("中序遍历: ");
        inorderRec(root);
        System.out.println();
    }

    private void inorderRec(AVLNode node) {
        if (node != null) {
            inorderRec(node.left);
            System.out.print(node.val + " ");
            inorderRec(node.right);
        }
    }

    // 验证是否为 AVL 树（调试用）
    public boolean isAVL() {
        return isAVLRec(root) != -1;
    }

    private int isAVLRec(AVLNode node) {
        if (node == null) return 0;

        int leftHeight = isAVLRec(node.left);
        if (leftHeight == -1) return -1;

        int rightHeight = isAVLRec(node.right);
        if (rightHeight == -1) return -1;

        if (Math.abs(leftHeight - rightHeight) > 1) {
            return -1; // 失衡
        }

        return 1 + Math.max(leftHeight, rightHeight);
    }

    public static void main(String[] args) {
        AVLTree avl = new AVLTree();

        // 插入导致 RR 失衡的序列：10, 20, 30
        avl.insert(10);
        avl.insert(20);
        avl.insert(30);

        avl.inorder(); // 输出: 10 20 30
        System.out.println("是 AVL 树? " + avl.isAVL()); // true

        // 继续插入
        avl.insert(40);
        avl.insert(50); // 此时会触发 RL 或 RR 旋转
        avl.insert(25);

        avl.inorder(); // 10 20 25 30 40 50
        System.out.println("高度平衡? " + avl.isAVL()); // true

        // 删除测试
        avl.delete(30);
        avl.inorder(); // 10 20 25 40 50
        System.out.println("删除后仍平衡? " + avl.isAVL()); // true
    }
}

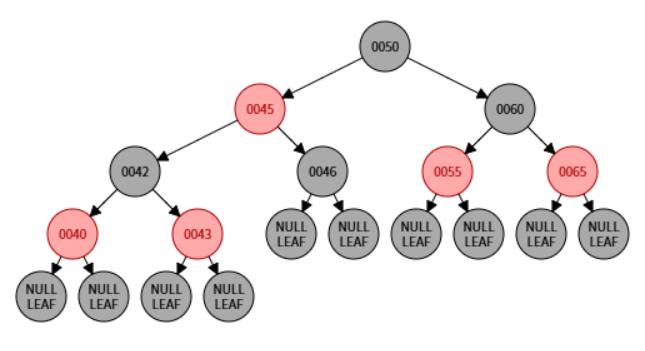
红黑树：工程实践的王者

红黑树是另一种自平衡二叉搜索树，它在AVL树的基础上做了一些”妥协”。它不像AVL树那样追求绝对平衡，而是通过一套更宽松的规则来保证大致平衡，从而减少在插入/删除时的旋转次数，在整体性能上取得了更好的工程实践效果。Java的 TreeMap、TreeSet 和 C++ STL 的 map、set 底层都使用了红黑树。

基本概念和特点：

  • 每个节点非红即黑。
  • 默认插入就是红色。
  • 根节点是黑色的。
  • 所有叶子节点（NIL空节点）都是黑色的。
  • 红色节点的子节点必须是黑色的（即不能有连续的红色节点）。
  • 从任一节点到其每个叶子节点的所有路径都包含相同数目的黑色节点。

规则 4 和 5 是红黑树平衡的关键。规则 5 保证了没有一条路径会比其他路径长出两倍以上，从而实现了大致平衡。

红黑树构成示意图

红黑树示意图

java实现红黑树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
package com.springdemo.demo.binarytree;

public class RedBlackTree<T extends Comparable<T>> {
    // 节点颜色枚举
    private enum Color {
        RED, BLACK
    }

    // 红黑树节点类
    private static class Node<T> {
        T value;
        Node<T> left;
        Node<T> right;
        Node<T> parent;
        Color color;

        public Node(T value) {
            this.value = value;
            this.color = Color.RED; // 插入默认红色
            this.left = null;
            this.right = null;
            this.parent = null;
        }
    }

    private Node<T> root;
    private final Node<T> NIL; // 空叶子节点（统一用一个NIL节点）

    public RedBlackTree() {
        NIL = new Node<>(null);
        NIL.color = Color.BLACK; // 空节点是黑色
        root = NIL;
    }


    // 1. 左旋转（核心平衡操作）
    private void leftRotate(Node<T> x) {
        Node<T> y = x.right;
        x.right = y.left;

        if (y.left != NIL) {
            y.left.parent = x;
        }
        y.parent = x.parent;

        if (x.parent == NIL) {
            root = y;
        } else if (x == x.parent.left) {
            x.parent.left = y;
        } else {
            x.parent.right = y;
        }
        y.left = x;
        x.parent = y;
    }


    // 2. 右旋转（核心平衡操作）
    private void rightRotate(Node<T> y) {
        Node<T> x = y.left;
        y.left = x.right;

        if (x.right != NIL) {
            x.right.parent = y;
        }
        x.parent = y.parent;

        if (y.parent == NIL) {
            root = x;
        } else if (y == y.parent.right) {
            y.parent.right = x;
        } else {
            y.parent.left = x;
        }
        x.right = y;
        y.parent = x;
    }


    // 3. 插入后修复红黑树规则
    private void insertFixup(Node<T> z) {
        // 父节点是红色才需要修复（红节点相邻）
        while (z.parent.color == Color.RED) {
            if (z.parent == z.parent.parent.left) { // 父节点是左孩子
                Node<T> uncle = z.parent.parent.right; // 叔叔节点

                if (uncle.color == Color.RED) { // 情况1：叔叔是红色
                    z.parent.color = Color.BLACK;
                    uncle.color = Color.BLACK;
                    z.parent.parent.color = Color.RED;
                    z = z.parent.parent;
                } else { // 叔叔是黑色
                    if (z == z.parent.right) { // 情况2：当前节点是右孩子
                        z = z.parent;
                        leftRotate(z);
                    }
                    // 情况3：当前节点是左孩子
                    z.parent.color = Color.BLACK;
                    z.parent.parent.color = Color.RED;
                    rightRotate(z.parent.parent);
                }
            } else { // 父节点是右孩子（镜像逻辑）
                Node<T> uncle = z.parent.parent.left;

                if (uncle.color == Color.RED) {
                    z.parent.color = Color.BLACK;
                    uncle.color = Color.BLACK;
                    z.parent.parent.color = Color.RED;
                    z = z.parent.parent;
                } else {
                    if (z == z.parent.left) {
                        z = z.parent;
                        rightRotate(z);
                    }
                    z.parent.color = Color.BLACK;
                    z.parent.parent.color = Color.RED;
                    leftRotate(z.parent.parent);
                }
            }
        }
        root.color = Color.BLACK; // 确保根节点是黑色
    }


    // 4. 插入节点
    public void insert(T value) {
        Node<T> z = new Node<>(value);
        Node<T> y = NIL;
        Node<T> x = root;

        // 找到插入位置（和普通BST插入逻辑一致）
        while (x != NIL) {
            y = x;
            if (z.value.compareTo(x.value) < 0) {
                x = x.left;
            } else {
                x = x.right;
            }
        }
        z.parent = y;

        if (y == NIL) {
            root = z; // 树为空，插入根节点
        } else if (z.value.compareTo(y.value) < 0) {
            y.left = z;
        } else {
            y.right = z;
        }

        // 初始化新节点的子节点为NIL
        z.left = NIL;
        z.right = NIL;
        insertFixup(z); // 插入后修复
    }


    // 中序遍历（验证树的有序性）
    public void inOrderTraversal() {
        inOrderHelper(root);
    }

    private void inOrderHelper(Node<T> node) {
        if (node != NIL) {
            inOrderHelper(node.left);
            System.out.print(node.value + "(" + node.color + ") ");
            inOrderHelper(node.right);
        }
    }


    // 测试示例
    public static void main(String[] args) {
        RedBlackTree<Integer> rbTree = new RedBlackTree<>();
        rbTree.insert(50);
        rbTree.insert(45);
        rbTree.insert(60);
        rbTree.insert(42);
        rbTree.insert(46);
        rbTree.insert(40);
        rbTree.insert(43);
        rbTree.insert(65);

        // 中序遍历（输出有序，同时显示节点颜色）
        System.out.println("中序遍历结果：");
        rbTree.inOrderTraversal();
    }
}

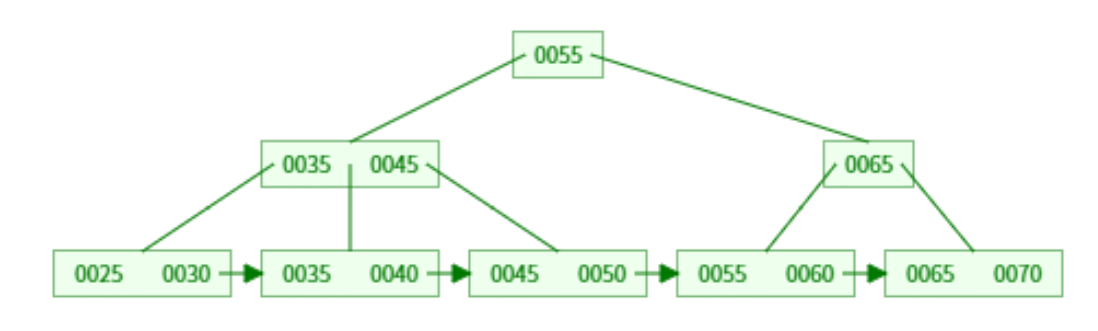
B树与B+树：磁盘存储的引擎

我们之前学的二叉搜索树、AVL 树、红黑树，全是为「内存中的数据查找」设计的，它们的优点是查询快（O(logn)），但有一个致命缺陷：

这类树的节点层级多、高度偏高，而且每次只能从一个节点跳转一个子节点。

而我们实际开发中，99% 的数据都存在硬盘 / 磁盘中（比如 MySQL 数据库、文件系统），磁盘的「寻址速度」极慢、「连续读数据」极快 ——硬盘最讨厌的就是「频繁寻址跳转」，最喜欢「一次性读一片数据」。

二叉树家族在磁盘场景下完全不适用：一次查询要跳十几次磁盘，速度慢到无法接受。

B 树的诞生唯一目的：为「磁盘 / 外存存储」量身设计的搜索树，最大化减少磁盘寻址次数，最大化利用磁盘的连续读取优势！

基本概念和特点：

  • 每个节点最多有 m 个子节点。
  • 每个非根、非叶子节点至少有 ⌈m/2⌉ 个子节点。
  • 根节点至少有2个子节点（除非它本身是叶子节点）。
  • 所有叶子节点都位于同一层。
  • 一个非叶子节点如果有 k 个子节点，则它包含 k-1 个键，这些键将子树的值域划分开。

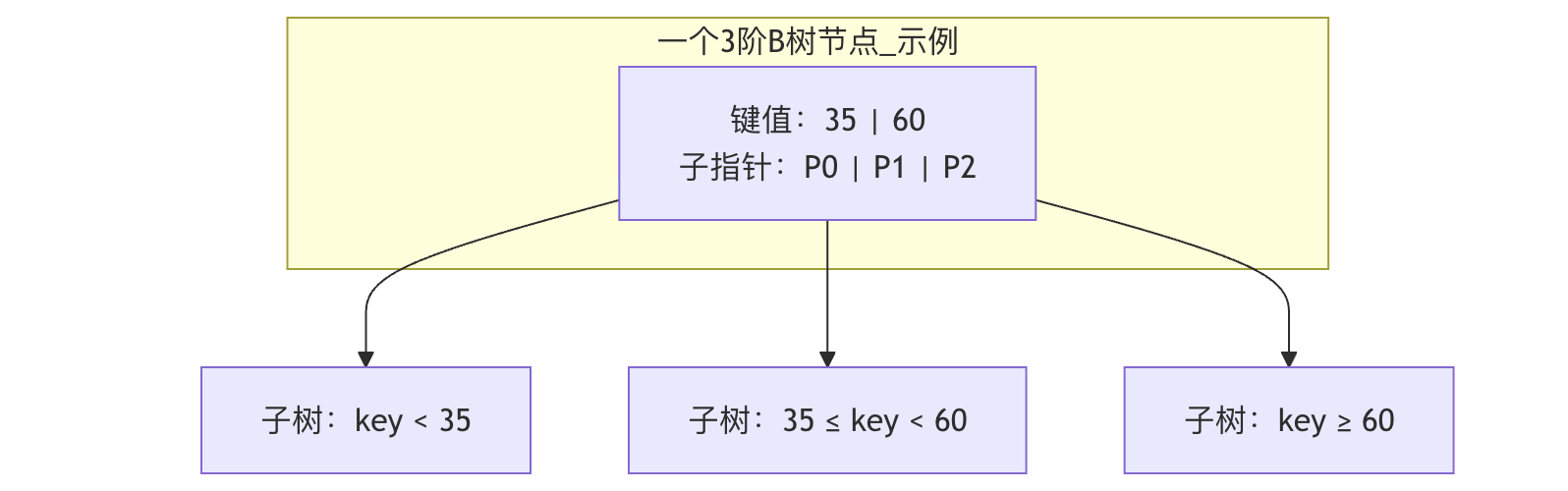
B树示意图

B树

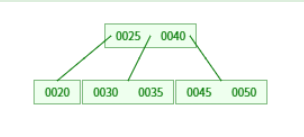
B 树的「矮胖」结构，完美适配磁盘的读写特性！

磁盘的两个核心特性：

  1. 磁盘的 寻址时间（找到数据在磁盘的位置）：极慢，一次寻址≈10ms；
  2. 磁盘的 连续读取时间（找到位置后读一片数据）：极快，读 1KB 和读 100KB 几乎一样快。

二叉树的致命缺点（磁盘场景）：

二叉树是「瘦高」的，比如存 100 万条数据，二叉树的高度大约是 20 层 → 意味着查询一次要 磁盘寻址 20 次 → 总耗时≈200ms，慢到无法接受。

B 树的极致优势（磁盘场景）：

B 树是「矮胖」的，节点能存大量数据，比如一个磁盘块能存 100 个关键字 → 100 万条数据的 B 树高度只有 34 层 → 查询一次只需要 **磁盘寻址 34 次** → 总耗时≈30ms，速度提升 6~7 倍！

本质：B 树把「多次磁盘寻址」变成「少量磁盘寻址」，把「零散读」变成「批量读」，这就是 B 树的封神之处。

B + 树是 B 树的优化升级版，核心设计目标是 更适配磁盘存储、更高效支持数据库的查询场景（单值查询、范围查询、排序等）。它的所有特点都围绕 “提升磁盘 IO 效率” 和 “优化查询体验” 展开。

基本概念和特点：

  1. 「数据只存叶子，索引只存非叶」—— 非叶子节点更 “轻”，树更矮胖

    • 特点细节：非叶子节点（根、中间层）：只存「关键字（索引）+ 子树指针」，不存完整数据（比如 MySQL 中不存行数据，只存主键值）；叶子节点：存「完整关键字 + 数据地址 / 完整数据」（MySQL 中叶子节点存整行数据或主键到行数据的指针）。

    • 对比 B 树：B 树的非叶子节点也存数据，导致一个节点能存的索引数量少，树更高。

    • 实际价值：非叶子节点更 “小”，一个磁盘块能装更多索引 → 树的高度比 B 树更低（比如 100 阶 B + 树存 1 亿数据，高度仅 3 层），磁盘寻址次数更少，查询更快。

  2. 「叶子节点全在同一层」—— 绝对平衡，查询时间稳定

    • 特点细节：和 B 树一样，所有叶子节点都处于树的最底层，没有 “深浅不一” 的情况。

    • 对比 B 树：两者一致，都是绝对平衡树（区别于红黑树的 “相对平衡”）。

    • 实际价值：任何数据的查询都要经过「根→中间层→叶子」的固定路径，查询时间复杂度永远是 O(logn)，没有最坏情况差异，数据库查询更稳定。

  3. 「叶子节点用链表串联」—— 范围查询 / 排序秒完成

    • 特点细节：所有叶子节点按关键字有序排列，并且用「双向链表」连接（比如 MySQL 的 B + 树叶子节点是双向链表）。

    • 对比 B 树：B 树的叶子节点没有链表，范围查询需要 “回溯父节点”，效率极低。

    • 实际价值

      • 范围查询（比如查主键 100~200 的行）：找到 100 的位置后，直接遍历叶子链表到 200，无需回退；
      • 排序查询（比如按主键排序）：直接遍历叶子链表，无需额外排序，效率碾压 B 树。

  4. 「关键字冗余存储」—— 非叶节点关键字是叶子节点的 “索引副本”

    • 特点细节：非叶子节点的所有关键字，都会在叶子节点中重复出现（比如非叶节点存了 “50”，叶子节点中也一定有 “50”）。

    • 对比 B 树：B 树的关键字只存一次，不存在冗余。

    • 实际价值：非叶节点只需要 “指引路径”，无需存数据，进一步压缩非叶节点大小，让树更矮胖；同时叶子节点包含所有关键字，遍历链表就能获取全量数据，无需依赖非叶节点。

  5. 「节点内关键字有序，支持二分查找」—— 节点内查询极快

    • 特点细节：每个节点（无论非叶还是叶子）的关键字都按升序 / 降序排列，查询时先对节点内关键字做二分查找，再决定走哪个指针。

    • 对比 B 树：两者一致，都是 “节点内二分 + 节点外指针跳转”。

    • 实际价值：节点内查询时间是 O(logk)（k 是节点内关键字数），几乎可以忽略（因为 k 通常是 100+，log2 (100)≈7），查询效率接近内存操作。

  6. 「适配磁盘 “预读” 机制」—— 最大化利用磁盘 IO 特性

    • 特点细节：B + 树的节点大小被设计为「一个磁盘块的大小」（比如 4KB），磁盘读取时会 “预读” 整个节点（磁盘预读机制：读取一个数据时，会顺带读取相邻的一批数据，减少寻址）。

    • 对比 B 树：B 树也能适配，但 B + 树的非叶节点更轻，预读的 “有效索引密度” 更高。

    • 实际价值：一次磁盘 IO 就能读取一个完整节点的所有索引，无需多次读取，进一步减少磁盘 IO 次数。

    B+树存储图