五天手撕数据结构之 —— 图论结构

在计算机科学中，图被广泛用于模拟社交网络（用户是点，好友关系是线）、网页链接（网页是点，超链接是线）、通信网络乃至路径规划等问题。

图就像是一张社交网络关系图：

  • 节点（顶点）：图中的基本单元
  • 边：连接两个顶点的线
  • 路径：顶点的序列
  • 度：顶点连接的边数
  • 权重：关系的强度（亲密度、互动频率等）

图的分类

图可以根据其边的特性分为多种类型，理解这些是掌握图论的基础。

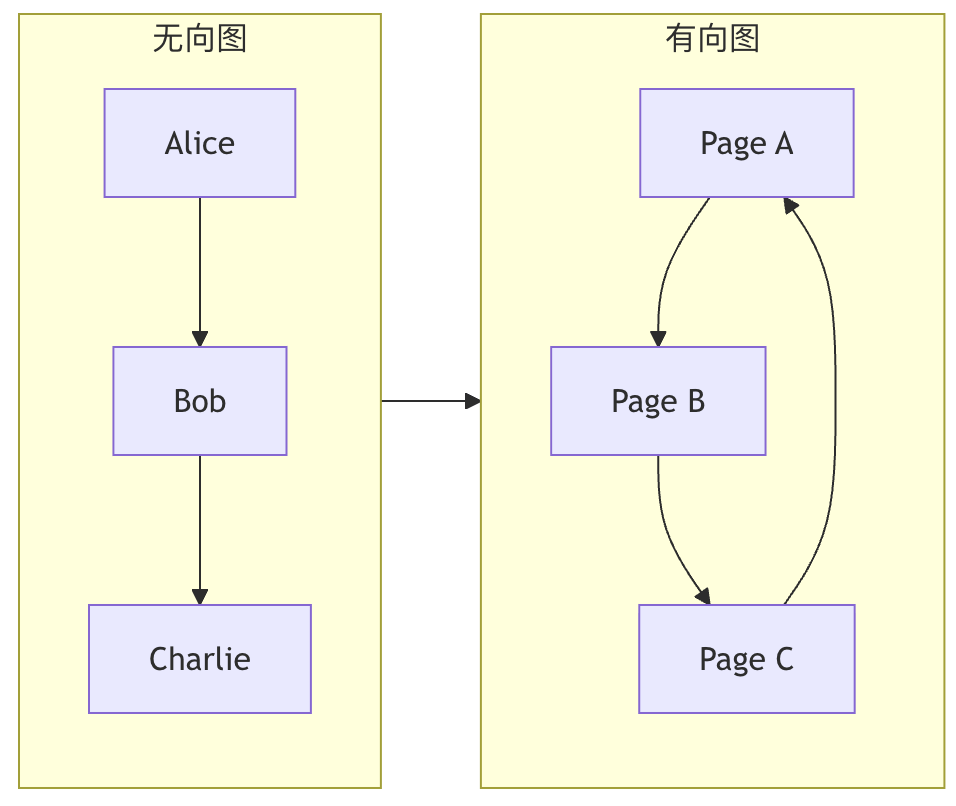
无向图 vs 有向图

类型 边（Edge）的特点 生活类比 示例
无向图 边没有方向，(A, B) 表示 A 和 B 互相连接。 双向友谊：如果 Alice 是 Bob 的朋友，那么 Bob 也一定是 Alice 的朋友。 社交网络中的好友关系、电路中的连接。
有向图 边有方向，A -> B 表示从 A 指向 B 的单向连接。 微博关注：你可以关注某人，但对方不一定关注你。 网页超链接、任务依赖关系、交通单行道。

image

图的存储方式

如何在计算机中表示一个图？主要有两种主流方法。

邻接矩阵

使用一个二维数组（矩阵）matrix 来表示图。matrix[i][j] 的值表示顶点 i 到顶点 j 的边的情况。

  • 对于无向图，矩阵是对称的。
  • 对于权重图，矩阵值存储权重（用特殊值如 0 或 ∞ 表示无边）。
  • 优点：检查任意两个顶点间是否有边非常快（O(1)）。
  • 缺点：占用空间大（O(V^2)），对于边数较少的 “稀疏图” 浪费空间。

邻接表

为每个顶点维护一个列表（链表、数组等），记录与其直接相连的所有顶点（及权重）。

  • 优点：空间效率高（O(V + E)），特别适合稀疏图。能快速找到一个顶点的所有邻居。
  • 缺点：检查任意两个顶点间是否有边较慢（O(degree(V))）。

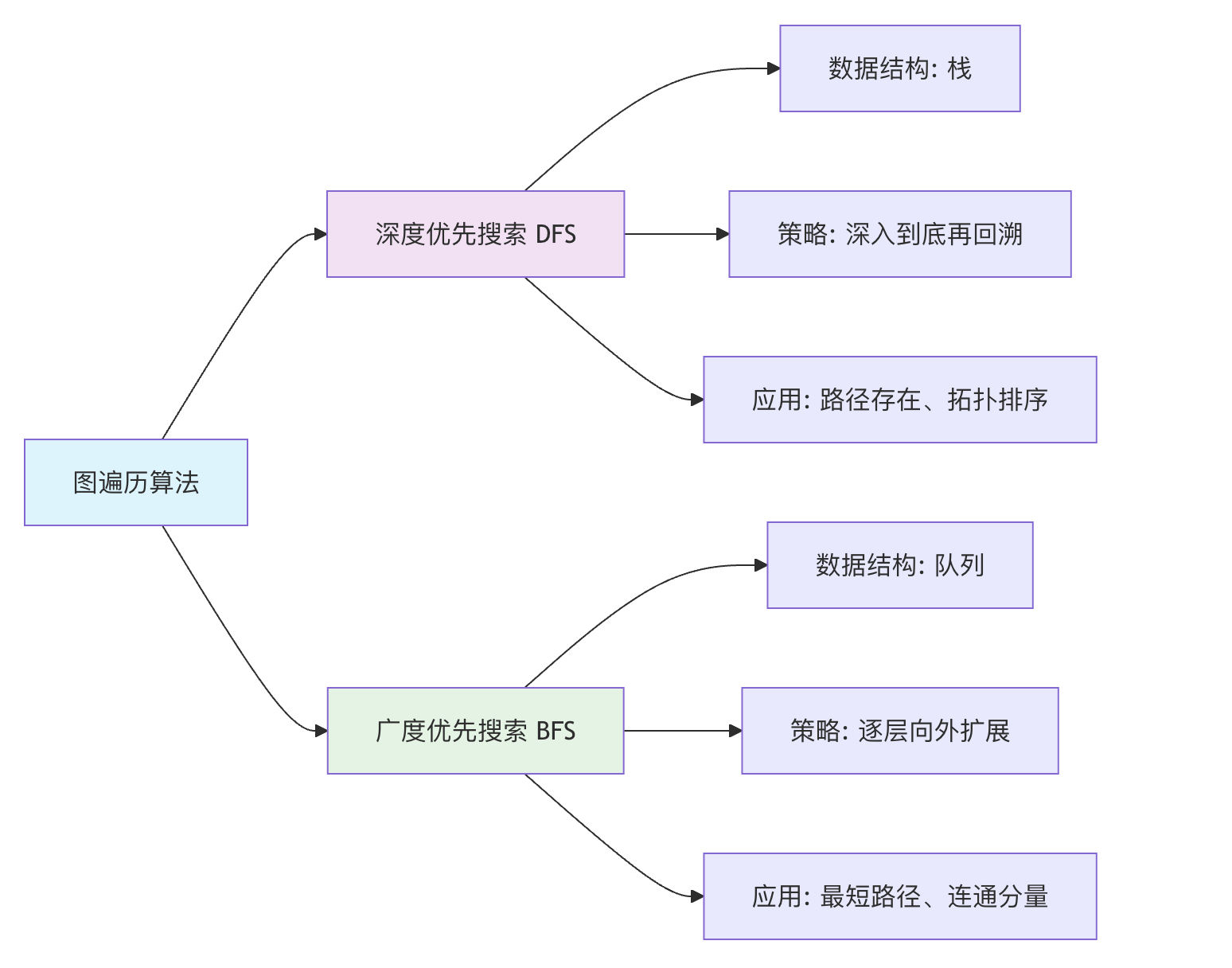
图的遍历算法

遍历是图算法的基础，意味着系统地访问图中的每一个顶点。

主要有两种策略：

广度优先搜索

广度优先搜索（BFS）像 “水波扩散” 一样，从起点开始，先访问所有直接邻居，再访问邻居的邻居，依此类推。它使用队列来实现。

算法步骤：

  1. 将起点放入队列并标记为已访问。

  2. 当队列不为空时：

    a. 取出队首顶点 v。

    b. 访问 v

    的所有未访问邻居，将它们放入队列并标记为已访问。

  3. 重复步骤 2。

深度优先搜索

深度优先搜索（DFS）像 “走迷宫” 一样，选择一条路走到尽头，然后回溯，再走另一条路。它使用栈（或递归）来实现。

递归算法步骤：

  1. 从顶点 v 开始，标记为已访问。

  2. 对于 v的每一个未访问邻居 u

    a. 递归调用 DFS(u)

image